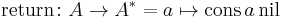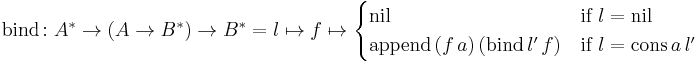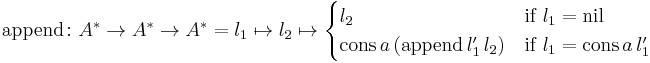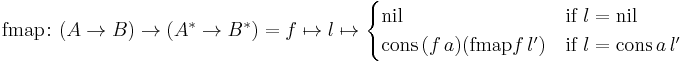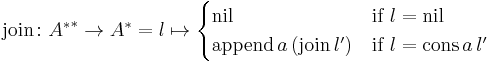List (abstract data type)

In computer science, a list or sequence is an abstract data type that implements an ordered collection of values, where the same value may occur more than once. An instance of a list is a computer representation of the mathematical concept of a finite sequence. Each instance of a value in the list is usually called an item, entry, or element of the list; if the same value occurs multiple times, each occurrence is considered a distinct item.

The name list is also used for several concrete data structures that can be used to implement abstract lists, especially linked lists.

The so-called static list structures allow only inspection and enumeration of the values. A mutable or dynamic list may allow items to be inserted, replaced, or deleted during the list's existence.

Many programming languages provide support for list data types, and have special syntax and semantics for lists and list operations. A list can often be constructed by writing the items in sequence, separated by commas, semicolons, or spaces, within a pair of delimiters such as parentheses '()', brackets, '[]', braces '{}', or angle brackets '<>'. Some languages may allow list types to be indexed or sliced like array types. In object-oriented programming languages, lists are usually provided as instances of subclasses of a generic "list" class. List data types are often implemented using arrays or linked lists of some sort, but other data structures may be more appropriate for some applications. In some contexts, such as in Lisp programming, the term list may refer specifically to a linked list rather than an array.

In type theory and functional programming, abstract lists are usually defined inductively by four operations: nil that yields the empty list, cons, which adds an item at the beginning of a list, head, that returns the first element of a list, and tail that returns a list minus its first element. Formally, Peano's natural numbers can be defined as abstract lists with elements of unit type.

1 Operations
2 Characteristics
3 Implementations
4 Programming language support
5 Applications
6 Abstract definition
- 6.1 The list monad
7 See also

Operations

Implementation of the list data structure may provide some of the following operations:

a constructor for creating an empty list;
an operation for testing whether or not a list is empty;
an operation for prepending an entity to a list
an operation for appending an entity to a list
an operation for determining the first component (or the "head") of a list
an operation for referring to the list consisting of all the components of a list except for its first (this is called the "tail" of the list.)

Characteristics

Lists have the following properties:

The size of lists. It indicates how many elements there are in the list.
Equality of lists:
- In mathematics, sometimes equality of lists is defined simply in terms of object identity: two lists are equal if and only if they are the same object.
- In modern programming languages, equality of lists is normally defined in terms of structural equality of the corresponding entries, except that if the lists are typed, then the list types may also be relevant.
Lists may be typed. This implies that the entries in a list must have types that are compatible with the list's type. It is common that lists are typed when they are implemented using arrays.
Each element in the list has an index. The first element commonly has index 0 or 1 (or some other predefined integer). Subsequent elements have indices that are 1 higher than the previous element. The last element has index <initial index> + <size> − 1.
- It is possible to retrieve the element at a particular index.
- It is possible to traverse the list in the order of increasing index.
- It is possible to change the element at a particular index to a different value, without affecting any other elements.
- It is possible to insert an element at a particular index. The indices of higher elements at that are increased by 1.
- It is possible to remove an element at a particular index. The indices of higher elements at that are decreased by 1.

Implementations

Lists are typically implemented either as linked lists (either singly or doubly linked) or as arrays, usually variable length or dynamic arrays.

The standard way of implementing lists, originating with the programming language Lisp, is to have each element of the list contain both its value and a pointer indicating the location of the next element in the list. This results in either a linked list or a tree, depending on whether the list has nested sublists. Some older Lisp implementations (such as the Lisp implementation of the Symbolics 3600) also supported "compressed lists" (using CDR coding) which had a special internal representation (invisible to the user). Lists can be manipulated using iteration or recursion. The former is often preferred in imperative programming languages, while the latter is the norm in functional languages.

Lists can be implemented as self-balancing binary search trees holding index-value pairs, providing equal-time access to any element (e.g. all residing in the fringe, and internal nodes storing the right-most child's index, used to guide the search), taking the time logarithmic in the list's size, but as long as it doesn't change much will provide the illusion of random access and enable swap, prefix and append operations in logarithmic time as well.

Programming language support

Some languages do not offer a list data structure, but offer the use of associative arrays or some kind of table to emulate lists. For example, Lua provides tables. Although Lua stores lists that have numerical indices as arrays internally, they still appear as hash tables.

In Lisp, lists are the fundamental data type and can represent both program code and data. In most dialects, the list of the first three prime numbers could be written as (list 2 3 5). In several dialects of Lisp, including Scheme, a list is a collection of pairs, consisting of a value and a pointer to the next pair (or null value), making a singly linked list.

Applications

As the name implies, lists can be used to store a list of records. The items in a list can be sorted for the purpose of fast search (binary search).

Because in computing, lists are easier to realize than sets, a finite set in mathematical sense can be realized as a list with additional restrictions, that is, duplicate elements are disallowed and such that order is irrelevant. If the list is sorted, it speeds up determining if a given item is already in the set but in order to ensure the order, it requires more time to add new entry to the list. In efficient implementations, however, sets are implemented using self-balancing binary search trees or hash tables, rather than a list.

Abstract definition

The abstract list type L with elements of some type E (a monomorphic list) is defined by the following functions:

nil: () → L

cons: E × L → L

first: L → E

rest: L → L

with the axioms

first (cons (e, l)) = e

rest (cons (e, l)) = l

for any element e and any list l. It is implicit that

cons (e, l) ≠ l

cons (e, l) ≠ e

cons (e₁, l₁) = cons (e₂, l₂) if e₁ = e₂ and l₁ = l₂

Note that first (nil ()) and rest (nil ()) are not defined.

These axioms are equivalent to those of the abstract stack data type.

In type theory, the above definition is more simply regarded as an inductive type defined in terms of constructors: nil and cons. In algebraic terms, this can be represented as the transformation 1 + E × L → L. first and rest are then obtained by pattern matching on the cons constructor and separately handling the nil case.

The list monad

The list type forms a monad with the following functions (using E^* rather than L to represent monomorphic lists with elements of type E):

$\text{return}\colon A \to A^{*} = a \mapsto \text{cons} \, a \, \text{nil}$

$\text{bind}\colon A^{*} \to (A \to B^{*}) \to B^{*} = l \mapsto f \mapsto \begin{cases} \text{nil} & \text{if} \ l = \text{nil}\\ \text{append} \, (f \, a) \, (\text{bind} \, l' \, f) & \text{if} \ l = \text{cons} \, a \, l' \end{cases}$

where append is defined as:

$\text{append}\colon A^{*} \to A^{*} \to A^{*} = l_1 \mapsto l_2 \mapsto \begin{cases} l_2 & \text{if} \ l_1 = \text{nil} \\ \text{cons} \, a \, (\text{append} \, l_1' \, l_2) & \text{if} \ l_1 = \text{cons} \, a \, l_1' \end{cases}$

Alternatively, the monad may be defined in terms of operations return, fmap and join, with:

$\text{fmap} \colon (A \to B) \to (A^{*} \to B^{*}) = f \mapsto l \mapsto \begin{cases} \text{nil} & \text{if} \ l = \text{nil}\\ \text{cons} \, (f \, a) (\text{fmap} f \, l') & \text{if} \ l = \text{cons} \, a \, l' \end{cases}$

$\text{join} \colon {A^{*}}^{*} \to A^{*} = l \mapsto \begin{cases} \text{nil} & \text{if} \ l = \text{nil}\\ \text{append} \, a \, (\text{join} \, l') & \text{if} \ l = \text{cons} \, a \, l' \end{cases}$

Note that fmap, join, append and bind are well-defined, since they're applied to progressively deeper arguments at each recursive call.

The list type is an additive monad, with nil as the monadic zero and append as monadic sum.

Lists form a monoid under the append operation. The identity element of the monoid is the empty list, nil. In fact, this is the free monoid over the set of list elements.